PROBLEMATIQUE PUISSANCE ET ENERGIE
1 / Le travail mécanique
1.1 / Estimation d’un travail à fournir
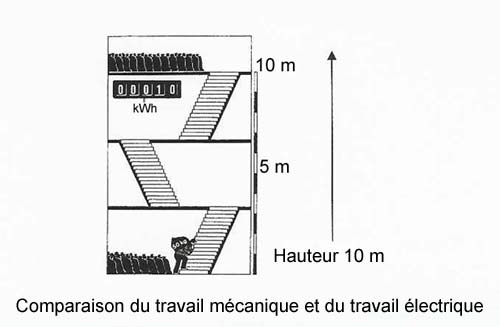
Combien faut-il monter de sacs de 50 kg sur une dénivellation de 10 m, pour accomplir un travail de 1 kWh, si on néglige le poids du corps ?
Pour répondre à ce problème, commençons par énoncé les paramètres du problème!
- 50kg => c’est la masse m du sac exprimé en gramme (g) qui permet de calculer le poids P (ou la force F) exercé par le sac en direction du sol.
Le poids/la force qui s’exprime en newton (N) dépend donc de la masse du sac m
et de l’accélération de la pesanteur « g » (au voisinage du sol, g vaut environ 10m/s²).
La formule à retenir :
F = m . g
- 10m => c’est la hauteur h exprimée en mètre (m).
Quand il s’agit d’un déplacement horizontal, celui-ci est noté l.
- 1kWh => c’est le travail W à fournir, c’est le déplacement à effectuer. Il est exprimé en watt heure (Wh).
Pour les petites valeurs, W s’exprime en Joule (j) ou en watt seconde (Ws).
La formule à retenir :
W = F . h
Dans l’énoncé le travail est exprimé en kWh (kilo Watt heure) au lieu de Ws (watt seconde)
- 1 joule (j) = 3600 Ws
- 1 kWh = 3600 000 Ws
1.2 / Résolution
Considérons une quantité de travail de référence Wref :
Wref= 1kWh = 360 000 Ws
Le travail à fournir pour monter un seul sac est :
W1 = F1 . h
= (m1 . g) . h
Le travail à fournir pour monter N sacs est :
WN = N . F1 . h
= N . (m1 . g) . h
Recherchons donc la quantité N de sac pour lesquels il faudrait fournir un travail WN de la même valeur que la quantité de référence Wref :
Wref = WN
= N . (m1
. g) . h
N = Wref/ [(m1 . g) . h]
Application
numérique:
Wref = 360 000 Ws
m1 = 50 kg²
g = 10 m/s²
h = 10 m
N = 360 000 / [(50 . 10) . 10]
N = 720 sacs
2 / Le énergie électrique
2.1 / Eclairage
Une lampe de 60 W est allumée 200 jours par année, 4 heures par jour.
Selon le tarif de l'entreprise électrique, 1 kWh coûte 20 centimes.
Combien d'énergie faut-il et que coûte l'énergie électrique pour 1 année d’utilisation?
Pour répondre à ce problème, commençons par énoncé les paramètres du problème!
- 60W => c’est la puissance P de la lampe elle s’exprime en watt (W)
La puissance c’est sa capacité à transformer en lumière un courant d’intensité I
lorsque cette lampe est alimenté sous une tension U.
La formule à retenir :
P = I . U (ou P = U . I)
- 200 jours/an, 4 heures/jour => c’est la durée de fonctionnent t que l’on exprimera en heure (h).
- 1 kWh => c’est l’énergie W exprimée en watt heure (Wh). En électricité l’énergie est notée E.
L’énergie E, c’est la quantité de courant d’intensité I, qui est transformé par la lampe
lorsqu’elle est alimentée sous la tension U pendant la durée t.
La formule à retenir :
E = I . U . t (ou E = U . I . t ou E = P . t)
- 20 centimes => c’est le coût de l’énergie (arbitraire) pour 1 kWh. On le notera « c » ce coût ?
1 euro = 100 centimes
2.2 / Résolution
- Durée t du fonctionnement en heure :
t = 200 (jours) . 4 (heure par jour)
= 800 h
- Quantité d’énergie E à fournir pour le fonctionnement souhaité (pendant une année) :
E = P . t
- Coût total Ct de l’énergie utilisé
Ct = c . E
Application numérique
P = 60 W
t = 800 h
c = 0,2 €
E = 60 . 800
= 48 kWh
Ct = 0,2 . 48
= 9,6 €