
Résistance d’un dipôle passif :
R = U/I unité : l’ohm (Ω)
Conductance d’un dipôle passif :
G = I/U = 1/R unité le siemens (s)
C’est un résistor (matériaux résistif) de deux bornes dont la caractéristique courant/tension U=f(I) est une droite passant par l’origine.
|
Résistance d’un dipôle passif : |
 Silec cables
Silec cables
Câbles électriques
La résistance d’un câble mono-conducteur peut se mesurer à l’aide d’un ohmmètre (monté en dérivation aux extrémités du câble), mais elle peut aussi se calculer si les trois paramètres qui la caractérisent sont connus :
R = ρ . l / s |
On retrouve cette situation dans le cas où on doit augmenter la longueur d’un câble après avoir déplacé un récepteur ou mis en place une nouveau. Exemple : Connexion à un câble de terre reliant un appareil et le piquet de terre.

La résistance série équivalente est la somme des résistances de chacun des câbles
Pour deux ou plus dipôles passifs raccordés en parallèle.
Exemple : Lampes d’éclairage ou de signalisation
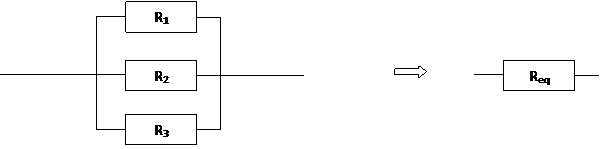
Cas particulier de deux résistances en parallèle

Les récepteurs que nous utilisons (dans le domestique) sont généralement conçus pour fonctionner sous une alimentation
standard (aspirateur 230v, télécommande 2x1,5v).
Entre les bornes d’alimentation de ces récepteurs il doit donc y avoir une différence de potentiel
(tension) suffisante pour que la quantité nécessaire de courant puisse être consommée.
De la même manière qu’il faut une bonne pression dans un tuyau d’arrosage pour acheminer l’eau
vers les plantes que l’on voudrait alimenter en eau !
Plus il y a pression, plus l’eau pourra être projetée loin…
Plus il y a de tension, plus la quantité de courant débité pourra être importante,
et de ce fait, plus de courant pourra être transformé en grandeur utile (chaleur, éclairage,…).

C'est à cause de cette différence de potentiel que la pile est capable de mettre en mouvement
les électrons libres, on parle alors de "force électromotrice" de la pile.
Voir l’animation avec une "pile Daniell"
(http://www.ostralo.net)
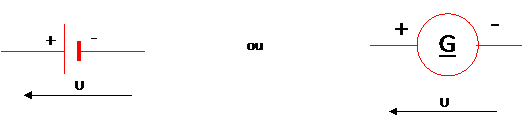

|
"Générateur virtuel" |

|
La tension sinusoïdale a une valeur qui varie de 0 volt à un maximum
(« pic + 325 volts pour la tension domestique), puis revient à 0 volt avec
une allure sinusoïdale. |
L’électromoteur est un dipôle qui peut soit fournir un courant soit en recevoir.
C’est le cas d’une pile rechargeable, mais aussi d’une machine électrique qui peut
fonctionner en moteur suite à l’entrainement en rotation de l’arbre de cette dernière
(lave linge, ascenseur,…) lorsqu’il est alimenté en électricité.
La machine électrique peut quand son arbre est entrainé en rotation (barrage hydraulique, éolienne,…)
fournir une tension à ses bornes.

L’électromoteur est remplacé par deux dipôles élémentaires en série :
– un résistor de résistance égale à la résistance interne r de l’électromoteur et représenté par le rectangle habituel ;
– une source de tension (parfaite) de valeur égale à la force électromotrice E de l’électromoteur et symbolisée par un cercle.
Cette source de tension est, bien sûr, orientée selon les polarités de l’électromoteur (du moins vers le plus).
Aux bornes du dipôle équivalent, la loi d’ohm générateur est vérifiée : U= E + ri. I
Aux bornes du dipôle équivalent, la loi d’ohm récepteur est vérifiée : U= E - ri. I
3 Panneaux photovoltaïques (à gauche) associés en série, puis les 4 groupes
de 3 panneaux associés en dérivation.
12 batteries d’accumulateurs à droite associés en série.
Il faut être prudent ! Le couplage en dérivation de plusieurs électromoteurs conduit souvent à des courants de circulation d’intensités d’autant plus importantes que les résistances internes sont faibles. Pour éviter cette circulation de courant entre les électromoteurs, ceux-ci sont choisis avec les même grandeurs caractéristiques (ri et E). Si des électromoteurs strictement identiques sont mis en dérivation, ils peuvent être remplacés par un seul électromoteur équivalent.


|
|
3 panneaux en série, de force électromotrice Ep=12 V |
|
4 ensembles de « 3 panneaux montés en série +, montés en dérivation : |
|
|
12 accumulateurs en série, de force électromotrice Eb=2 V. |
|
|

 e-Learning tools for Electrical Engineering
e-Learning tools for Electrical Engineering
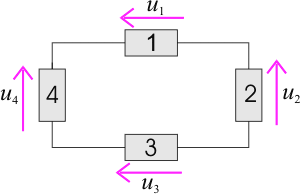
Figure 1 – Schéma représentatif de la Loi des Mailles
Compte tenu du sens de référence des tensions indiqué sur la Figure 1 et en additionnant les tensions dans le sens des aiguilles d'une montre, la loi des mailles permet d'écrire :
On a considéré ici l'opposé des tensions u2 et u4 car leur sens de référence est à l'opposé
du sens de circulation dans la maille.
Le fait d'avoir choisi un sens de circulation anti-horaire n'est cependant pas déterminant.
Si on avait choisi un sens horaire, on aurait obtenu une équation
différente mais rigoureusement équivalente.
 e-Learning tools for Electrical Engineering
e-Learning tools for Electrical Engineering
Dire que la somme des tensions le long d'une maille est nulle, revient à dire
que le travail nécessaire pour déplacer une charge le long d'une maille est nul.
En d'autres termes, cela veut dire que le système est "conservatif" : le travail fourni
par d'éventuelles sources présentes au sein de la maille pour déplacer une charge,
est absorbé par les récepteurs présents au sein de cette m ême maille.
Pour le circuit de la Figure 2, l'application de la loi des mailles permet d'écrire :
Pour la maille rouge et un sens de circulation anti-horaire : u1 - u2 + u3 = 0
Pour la maille bleue et un sens de circulation anti-horaire : u1 - u2 + u2 = 0
Pour la maille verte et un sens de circulation anti-horaire : u2 - u3 = 0
Cette loi se déduit facilement de la notion de courant électrique.
Supposons que l'on ait un flux i0=dq1/dt d'électrons
dans un conducteur arrivant à un "embranchement" d'un circuit électrique :
|
|
Les électrons venant de la "gauche" partiront soit dans la première, soit dans la deuxième branche.
Mais le nombre total d'électrons par seconde restera le même que celui qui arrive en permanence
par la gauche, et donc i0=i1+i2.
Un nœud est un point de convergence de plusieurs conducteurs.
Plus généralement, si on considère n conducteurs arrivant au même point O, avec les sens positifs des courants in définis comme suit, vers O...
|
|
La loi des nœuds stipule alors que la somme algébrique des courants arrivant à un nœud est constamment nulle :
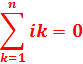
Dans un circuit complexe, il est possible de calculer les différences de potentiel aux bornes de chaque
résistance et l'intensité du courant continu dans chaque branche de circuit en appliquant les deux
lois de Kirchhoff : la loi des œuds et la loi des mailles.
Pour approfondir la résolution des équations en électronique, ces deux lois sont complétées par deux autres :
|
|